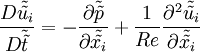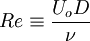Introduction to turbulence/Wall bounded turbulent flows
From CFD-Wiki
(→REVIEW OF LAMINAR BOUNDARY LAYERS) |
(→REVIEW OF LAMINAR BOUNDARY LAYERS) |
||
| Line 57: | Line 57: | ||
</td><td width="5%">(1)</td></tr></table> | </td><td width="5%">(1)</td></tr></table> | ||
| - | where <math>\tilde{\tilde{u_{i}}} \equiv u_{i}/U_{0}</math>, <math>\tilde{\tilde{x_{i}}} \equiv x_{i} / D</math>, <math>\tilde{\tilde{t}} \equiv U_{0} t / D</math> and <math>\tilde{\tilde{p}} \equiv p / \left( \rho U^{2}_{0} \right) </math> | + | where <math>\tilde{\tilde{u_{i}}} \equiv u_{i}/U_{0}</math>, <math>\tilde{\tilde{x_{i}}} \equiv x_{i} / D</math>, <math>\tilde{\tilde{t}} \equiv U_{0} t / D</math> and <math>\tilde{\tilde{p}} \equiv p / \left( \rho U^{2}_{0} \right) </math>. The kinematic viscosity, <math>\nu</math> has disappeared entirely, and is included in the '''Reynolds number''' defined by: |
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | :<math> | ||
| + | Re \equiv \frac{U_{o} D}{\nu} | ||
| + | </math> | ||
| + | </td><td width="5%">(2)</td></tr></table> | ||
Revision as of 09:07, 14 August 2011
WALL-BOUNDED TURBULENT FLOWS
Introduction
Without the presence of walls or surfaces, turbulence in the absence of density fluctuations could not exist. This is because it is only at surfaces that vorticity can actually be generated by an on-coming flow is suddenly brought to rest to satisfy the no-slip condition. The vorticity generated at the leading edge can then be diffused, transported and amplified. But it can only be generated at the wall, and then only at the leading edge at that. Once the vorticity has been generated, some flows go on to develop in the absence of walls, like the free shear flows we considered earlier. Other flows remained “attached” to the surface and evolve entirely under the influence of it. These are generally referred to as “wall-bounded flows” or “boundary layer flows”. The most obvious causes for the effects of the wall on the flow arise from the wall-boundary conditions. In particular,
- The kinematic boundary condition demands that the normal velocity of
the fluid on the surface be equal to the normal velocity of the surface. This means there can be no-flow through the surface. Since the velocity normal to the surface cannot just suddenly vanish, the kinematic boundary condition ensures that the normal velocity components in wall-bounded flows are usually much less than in free shear flows. Thus the presence of the wall reduces the entrainment rate. Note that viscosity is not necessary in the equations to satisfy this condition, and it can be met even by solutions to to the inviscid Euler’s equations.
- The no-slip boundary condition demands that the velocity component tangential to the wall be the same as the tangential velocity of the wall. If the
wall is at rest relative, then the no-slip condition demands the tangential flow velocity be identically zero at the surface.
Figure 8.1: Flow around a simple airfoil without separation.
It is the no-slip condition, of course, that led Ludwig Prandtl1 to the whole
idea of a boundary layer in the first place. Professor Prandt literally saved fluid mechanics from d’Alembert’s paradox: the fact that there seemed to be no drag in an inviscid fluid (not counting form drag). Prior to Prandtl, everyone thought that as the Reynolds number increased, the flow should behave more and more like an inviscid fluid. But when there were surfaces, it clearly didn’t. Instead of behaving like those nice potential flow solutions (like around cylinders, for example), the flow not only produced drag, but often separated and produced wakes and other free shear flows. Clearly something was very wrong, and as a result fluid mechanics didn’t get much respect from engineers in the 19th century.
And with good reason: how useful could a bunch of equations be if they couldn’t
find viscous drag, much less predict how much. But Prandtl’s idea of the boundary
layer saved everything.
Prandtl’s great idea was the recognition that the viscous no-slip condition could not be met without somehow retaining at least one viscous stress term in the equations. As we shall see below, this implies that there must be at least two length scales in the flow, unlike the free shear flows we considered in the previous chapter for which the mean flow could be characterized by only a single length scale. The second length scale characterizes changes normal to the wall, and make it clear precisely which viscous term in the instantaneous equations is important.
REVIEW OF LAMINAR BOUNDARY LAYERS
Let’s work this all out for ourselves by considering what happens if we try to
apply the kinematic and no-slip boundary conditions to obtain solutions of the
Navier-Stokes equations in the infinite Reynolds number limit. Let’s restrict our
attention for the moment to the laminar flow of a uniform stream of speed, 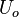 ,
around a body of characteristic dimension, D, as shown in Figure 8.1. It is easy
to see the problem if we non-dimensionalize our equations using the free stream
boundary condition and body dimension. The result is:
,
around a body of characteristic dimension, D, as shown in Figure 8.1. It is easy
to see the problem if we non-dimensionalize our equations using the free stream
boundary condition and body dimension. The result is:
|
| (1) |
where  ,
, 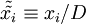 ,
, 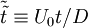 and
and 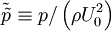 . The kinematic viscosity,
. The kinematic viscosity, 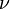 has disappeared entirely, and is included in the Reynolds number defined by:
has disappeared entirely, and is included in the Reynolds number defined by:
|
| (2) |