Turbulence dissipation rate
From CFD-Wiki
(Difference between revisions)
(Finally fixed the \nu and \equiv problems in the LaTeX rendering) |
Pete Bachant (Talk | contribs) (Abbreviations for units no longer italicized.) |
||
| (2 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | Turbulence dissipation, <math>\epsilon</math> is the rate at which [[turbulence kinetic energy]] is converted into thermal internal energy. The SI unit of <math>\epsilon</math> is <math>J / kg s = m^2 / s^3</math>. | + | Turbulence dissipation, <math>\epsilon</math> is the rate at which [[turbulence kinetic energy]] is converted into thermal internal energy. The SI unit of <math>\epsilon</math> is <math>\mathrm{J} / (\mathrm{kg} \cdot \mathrm{s}) = \mathrm{m}^2 / \mathrm{s}^3</math>. |
<math>\epsilon \, \equiv \, \nu \overline{\frac{\partial u_i'}{\partial x_k}\frac{\partial u_i'}{\partial x_k}}</math> | <math>\epsilon \, \equiv \, \nu \overline{\frac{\partial u_i'}{\partial x_k}\frac{\partial u_i'}{\partial x_k}}</math> | ||
| + | |||
| + | |||
| + | For compressible flows the definition is most often slightly different: | ||
| + | |||
| + | <math>\epsilon \, \equiv \, \frac{1}{\overline{\rho}} \overline{\tau_{ij} \frac{\partial u_i''}{\partial x_j}}</math> | ||
| + | |||
| + | Where the viscous stress, <math>\tau_{ij}</math>, using Stokes law for mono-atomic gases, is given by: | ||
| + | |||
| + | <math>\tau_{ij} = 2 \mu S^*_{ij}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | <math>S^*_{ij} \equiv \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij}</math> | ||
Latest revision as of 01:00, 11 April 2015
Turbulence dissipation, 
is the rate at which turbulence kinetic energy is converted into thermal internal energy. The SI unit of is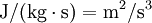 
.
For compressible flows the definition is most often slightly different:
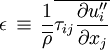
Where the viscous stress,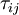 
, using Stokes law for mono-atomic gases, is given by:
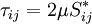
where
