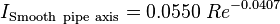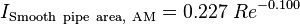Turbulence boundary conditions
From CFD-Wiki
| Line 11: | Line 11: | ||
:<math>k_{AA} = U_m^2 \; I_{AA}^2</math> | :<math>k_{AA} = U_m^2 \; I_{AA}^2</math> | ||
:<math>\epsilon_{AA} = C_{\mu,AA}^\frac{3}{4} \times \frac{k_{AA}^\frac{3}{2}}{l_{AA}}</math> | :<math>\epsilon_{AA} = C_{\mu,AA}^\frac{3}{4} \times \frac{k_{AA}^\frac{3}{2}}{l_{AA}}</math> | ||
| - | |||
| - | |||
The model parameters <math>\kappa_g</math>, <math>A_g</math>, <math>B_g</math> and <math>C_g</math> can be computed using the following function: | The model parameters <math>\kappa_g</math>, <math>A_g</math>, <math>B_g</math> and <math>C_g</math> can be computed using the following function: | ||
| Line 32: | Line 30: | ||
| <math>C_g / \sqrt{Re_\tau}</math> || style="text-align:right;"|1.03 || style="text-align:right;"|-0.91|| style="text-align:right;"|3.30e-5 || style="text-align:right;"|-11755 | | <math>C_g / \sqrt{Re_\tau}</math> || style="text-align:right;"|1.03 || style="text-align:right;"|-0.91|| style="text-align:right;"|3.30e-5 || style="text-align:right;"|-11755 | ||
|} | |} | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
:<math>\delta</math> is the boundary layer thickness, which in fully developed pipe flow is the radius, or half the [[hydraulic diameter]]. | :<math>\delta</math> is the boundary layer thickness, which in fully developed pipe flow is the radius, or half the [[hydraulic diameter]]. | ||
Revision as of 23:23, 1 December 2024
This section is under construction, please do not trust the information available here yet
Introduction
Fully developed turbulent pipe-flow inlet
For fully developed turbulent pipe flow the turbulence inlet properties can be estimated using the model presented by Basse in Table 1 of [10].
The model parameters 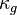 ,
,  ,
,  and
and  can be computed using the following function:
can be computed using the following function:
Where the a, b, c and d constants have been fitted using Princeton Superpipe measurements [2]:
| Parameter | a | b | c | d |
|---|---|---|---|---|
 | −1.18 | 1.52 | 2.15e-4 | -8786 |
 | 2.21 | -0.60 | 3.97e-5 | 11186 |
 | 1.28 | -0.32 | 5.85e-5 | 4609 |
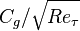 | 1.03 | -0.91 | 3.30e-5 | -11755 |
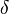 is the boundary layer thickness, which in fully developed pipe flow is the radius, or half the hydraulic diameter.
is the boundary layer thickness, which in fully developed pipe flow is the radius, or half the hydraulic diameter.
Information below is old and will be reformulated
For fully developed duct flow the turbulence intensity at the core can be estimated as [1]:
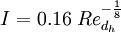 ,
,
where 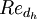 is the Reynolds number based on the pipe hydraulic diameter
is the Reynolds number based on the pipe hydraulic diameter 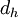 . Additional details on the derivation can be found in [2].
. Additional details on the derivation can be found in [2].
Russo and Basse published a paper [3] where they derive turbulence intensity scaling laws based on CFD simulations and Princeton Superpipe measurements. The turbulence intensity over the pipe area is defined as an arithmetic mean (AM). The measurement-based scaling laws are:
Scaling using other turbulence intensity definitions is investigated in [4,5]. Here, it is also found that turbulence intensity scales with the friction factor, both for smooth- and rough-wall pipe flow. Code for an example in [5] can be found in [6]. A high Reynolds number transition in the scaling has been characterized in [7,8]. Turbulence intensity scaling extrapolated to extreme Reynolds numbers is studied in [9].
References
[1] ANSYS, Inc. (2022), "ANSYS Fluent User's Guide, Release R1", Equation (7.71).
[2] Basse, N.T. (2022), "Mind the Gap: Boundary Conditions for Turbulence Modelling", https://www.researchgate.net/publication/359218404_Mind_the_Gap_Boundary_Conditions_for_Turbulence_Modelling.
[3] Russo, F. and Basse, N.T. (2016), "Scaling of turbulence intensity for low-speed flow in smooth pipes", Flow Meas. Instrum., vol. 52, pp. 101–114.
[4] Basse, N.T. (2017), "Turbulence intensity and the friction factor for smooth- and rough-wall pipe flow", Fluids, vol. 2, 30.
[5] Basse, N.T. (2019), "Turbulence intensity scaling: A fugue", Fluids, vol. 4, 180.
[6] Basse, N.T. (2019), "Python code to calculate turbulence intensity based on Reynolds number and surface roughness.", https://www.researchgate.net/publication/336374461_Python_code_to_calculate_turbulence_intensity_based_on_Reynolds_number_and_surface_roughness.
[7] Basse, N.T. (2021), "Scaling of global properties of fluctuating and mean streamwise velocities in pipe flow: Characterization of a high Reynolds number transition region", Physics of Fluids, vol. 33, 065127.
[8] Basse, N.T. (2021), "Scaling of global properties of fluctuating streamwise velocities in pipe flow: Impact of the viscous term", Physics of Fluids, vol. 33, 125109.
[9] Basse, N.T. (2022), "Extrapolation of turbulence intensity scaling to Re_tau>>10^5", Physics of Fluids, vol. 34, 075128.
[10] Basse, N.T. (2023), "An Algebraic Non-Equilibrium Turbulence Model of the High Reynolds Number Transition Region", Water 2023, 15, 3234. https://doi.org/10.3390/w15183234.
[11] Basse, N.T. (2023), "Supplementary Information: An algebraic non-equilibrium turbulence model of the high Reynolds number transition region", https://www.researchgate.net/publication/373108195_Supplementary_Information_An_algebraic_non-equilibrium_turbulence_model_of_the_high_Reynolds_number_transition_region.
[12] Hultmark M, Vallikivi M, Bailey SCC and Smits AJ. (2013), "Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow", J. Fluid Mech. 728, 376-395.

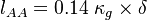
![I_{AA} = \sqrt{\left[ B_g + \frac{3}{2} A_g - \frac{8 C_g}{\sqrt[3]{Re_\tau}}\right] \times \frac{\lambda}{8}}](/W/images/math/f/1/d/f1db22892fa4335d5f9e76873c2ab47d.png)
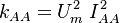
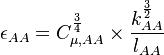
![Q(Re_\tau) = a + b \cdot tanh(c \cdot [Re_\tau - d])](/W/images/math/b/0/7/b07b24c846c7110e6d98deff6ce2ad88.png)