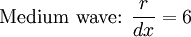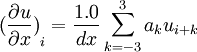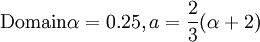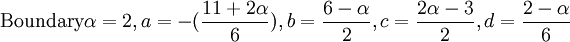Linear wave propagation
From CFD-Wiki
(Difference between revisions)
| Line 3: | Line 3: | ||
</math> | </math> | ||
== Domain == | == Domain == | ||
| - | x=[ | + | :<math> x=[-10,10] </math> |
== Initial Condition == | == Initial Condition == | ||
| - | :<math> u(x,0)= | + | :<math> u(x,0)=exp[-ln(2){(\frac{x-x_c}{r})}^2]</math> |
== Boundary condition == | == Boundary condition == | ||
| - | u | + | :<math>u(-10)=0</math> |
== Exact solution == | == Exact solution == | ||
| - | :<math> u(x, | + | :<math> u(x,0)=exp[-ln(2){(\frac{x-x_c-ct}{r})}^2]</math> |
== Numerical method == | == Numerical method == | ||
| - | c=1,t=0.25 | + | :<math>c=1,dx=1/6,dt=0.5dx,t=7.5</math> |
| + | :<math> \mbox{Long wave :}\frac{r}{dx}=20</math> | ||
| + | :<math> \mbox{Medium wave: }\frac{r}{dx}=6</math> | ||
| + | :<math> \mbox{Short wave : } \frac{r}{dx}=3</math> | ||
| + | === Space === | ||
| + | ==== Explicit Scheme (DRP)==== | ||
| + | :<math> {(\frac{\partial u}{\partial x})}_i=\frac{1.0}{dx}\sum_{k=-3}^3 a_k u_{i+k} </math> | ||
| + | The coefficients can be found in Tam(1992).At the right boundaries use fourth order central difference and fourth backward difference.At left boundaries use second order central difference for i=2 and fourth order central difference for i=3.The Dispersion relation preserving (DRP) finite volume scheme can be found in Popescu (2005). | ||
| + | ====Implicit Scheme(Compact)==== | ||
| + | :Domain: <math>\alpha v_{i-1} + v_i + \alpha v_{i+1}=\frac{a}{2h}(u_{i+1}-u_{i-1}) </math> | ||
| + | :Boundaries: <math> v_1+\alpha v_2=\frac{1}{h}(au_1+bu_2+cu_3+du_4) </math> | ||
| + | where v refers to the first derivative.For a general treatment of compact scheme refer to Lele (1992).In this test case the following values are used | ||
| + | :<math> \mbox{Domain} \alpha=0.25 , a=\frac{2}{3}(\alpha+2) </math> | ||
| + | :<math> \mbox{Boundary} \alpha=2 ,a=-(\frac{11+2\alpha}{6}),b=\frac{6-\alpha}{2},c=\frac{2\alpha-3}{2},d=\frac{2-\alpha}{6} </math> | ||
| + | |||
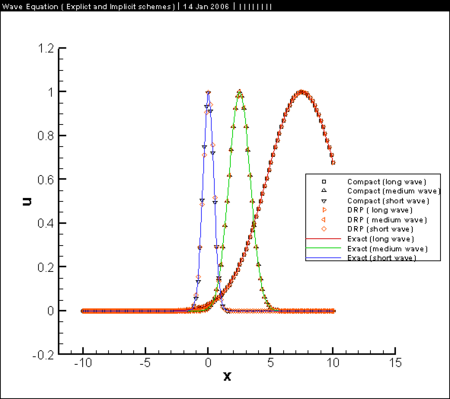
== Results == | == Results == | ||
| + | |||
[[Image:Initial_condition.png|450px]] | [[Image:Initial_condition.png|450px]] | ||
[[Image:Result_wave.png|450px]] | [[Image:Result_wave.png|450px]] | ||
== Reference == | == Reference == | ||
Revision as of 07:14, 14 January 2006
Contents |
Problem definition
Domain
Initial Condition
Boundary condition
Exact solution
Numerical method
Space
Explicit Scheme (DRP)
The coefficients can be found in Tam(1992).At the right boundaries use fourth order central difference and fourth backward difference.At left boundaries use second order central difference for i=2 and fourth order central difference for i=3.The Dispersion relation preserving (DRP) finite volume scheme can be found in Popescu (2005).
Implicit Scheme(Compact)
- Domain:

- Boundaries:
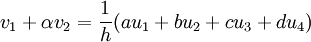
where v refers to the first derivative.For a general treatment of compact scheme refer to Lele (1992).In this test case the following values are used

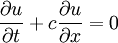
![x=[-10,10]](/W/images/math/1/b/1/1b14c536c4db5da52bbdcfe07f70db81.png)
![u(x,0)=exp[-ln(2){(\frac{x-x_c}{r})}^2]](/W/images/math/b/3/8/b38fab63c854b1f256b78d925988a116.png)
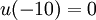
![u(x,0)=exp[-ln(2){(\frac{x-x_c-ct}{r})}^2]](/W/images/math/a/b/0/ab0b51feabf18adf6c4177f6cc507732.png)