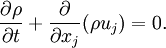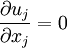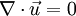Continuity equation
From CFD-Wiki
(Difference between revisions)
(new article) |
|||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| - | In [[fluid dynamics]], | + | In [[fluid dynamics]], the '''continuity equation''' is an expression of conservation of mass. In (vector) differential form, it is written as |
| - | :<math> {\partial \rho \over \partial t} + \nabla \cdot (\rho \ | + | :<math> {\partial \rho \over \partial t} + \nabla \cdot (\rho \vec{u}) = 0.</math> |
| - | where <math> \rho </math> is density, t is time, and | + | where <math> \rho </math> is density, <math>t</math> is time, and <math>\vec{u}</math> is fluid velocity. In cartesian tensor notation, it is written as |
| + | |||
| + | :<math> {\partial \rho \over \partial t} + {\partial \over \partial x_j}(\rho u_j) = 0.</math> | ||
| + | |||
| + | For incompressible flow, the density drops out, and the resulting equation is | ||
| + | |||
| + | :<math> {\partial u_j\over \partial x_j} = 0</math> | ||
| + | |||
| + | in tensor form or | ||
| + | |||
| + | :<math> \nabla \cdot \vec{u} = 0</math> | ||
| + | |||
| + | in vector form. The left-hand side is the divergence of velocity, and it is sometimes said that an incompressible flow is divergence free. | ||
<!-- | <!-- | ||
The '''law of conservation of mass/matter''' (The [[Lomonosov]]-[[Lavoisier]] law) states that the [[mass]] of a [[closed system]] of substances will remain constant, regardless of the processes acting inside the system. An equivalent statement is that [[matter]] changes form, but cannot be created or destroyed. This implies that for any chemical process in a closed system, the mass of the reactants must equal the mass of the products'''. | The '''law of conservation of mass/matter''' (The [[Lomonosov]]-[[Lavoisier]] law) states that the [[mass]] of a [[closed system]] of substances will remain constant, regardless of the processes acting inside the system. An equivalent statement is that [[matter]] changes form, but cannot be created or destroyed. This implies that for any chemical process in a closed system, the mass of the reactants must equal the mass of the products'''. | ||
--> | --> | ||
Latest revision as of 16:30, 25 May 2007
In fluid dynamics, the continuity equation is an expression of conservation of mass. In (vector) differential form, it is written as
where 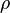 is density,
is density, 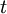 is time, and
is time, and 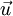 is fluid velocity. In cartesian tensor notation, it is written as
is fluid velocity. In cartesian tensor notation, it is written as
For incompressible flow, the density drops out, and the resulting equation is
in tensor form or
in vector form. The left-hand side is the divergence of velocity, and it is sometimes said that an incompressible flow is divergence free.