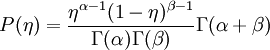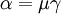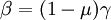Beta PDF
From CFD-Wiki
(Difference between revisions)
m (Reverted edits by ChierBasal (Talk) to last version by Hannes79) |
|||
| (2 intermediate revisions not shown) | |||
| Line 6: | Line 6: | ||
The beta function PDF has the form | The beta function PDF has the form | ||
:<math> | :<math> | ||
| - | P (\eta) = \frac{\eta^ | + | P (\eta) = \frac{\eta^{\alpha-1} (1- \eta)^{\beta-1}}{\Gamma(\alpha) \Gamma(\beta)} |
\Gamma(\alpha + \beta) | \Gamma(\alpha + \beta) | ||
</math> | </math> | ||
Latest revision as of 10:05, 17 December 2008
A 
probability density function depends on
two moments only; the mean 
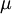and the variance 
.
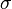This function is widely used in turbulent combustion to define the scalar distribution at each
computational point as a function of the mean and variance.
Assuming that the sample space of the scalar varies betwen 0 and 1.
The beta function PDF has the form
where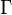 
is the gamma function and the parameters
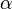and 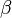are related through
where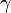 
is
