Skin friction coefficient
From CFD-Wiki
(→To do) |
|||
| (9 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
Where <math>\tau_w</math> is the local [[wall shear stress]], <math>\rho</math> is the fluid density and <math>U_\infty</math> is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet). | Where <math>\tau_w</math> is the local [[wall shear stress]], <math>\rho</math> is the fluid density and <math>U_\infty</math> is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet). | ||
| - | For a turbulent boundary layer several approximation formulas for the local skin friction can be used: | + | For a turbulent boundary layer several approximation formulas for the local skin friction for a flat plate can be used: |
1/7 power law: | 1/7 power law: | ||
| - | <math>C_f = 0.0576 Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7 </math> | + | :<math>C_f = 0.0576 Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7 </math> |
| - | 1/7 power law with experimental calibration (equation 21.12 in [ | + | 1/7 power law with experimental calibration (equation 21.12 in [[#References|[3]]]): |
| - | <math>C_f = 0.0592 \, Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7</math> | + | :<math>C_f = 0.0592 \, Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7</math> |
| - | Schlichting (equation 21.16 footnote in [ | + | Schlichting (equation 21.16 footnote in [[#References|[3]]]) |
| - | <math>C_f = [ 2 \, | + | :<math>C_f = [ 2 \, log_{10}(Re_x) - 0.65 ] ^{-2.3} \quad \mbox{for} \quad Re_x < 10^9 </math> |
| - | Schultz-Grunov (equation 21.19a in [ | + | Schultz-Grunov (equation 21.19a in [[#References|[3]]]): |
| - | <math>C_f = 0.370 \, [ | + | :<math>C_f = 0.370 \, [ log_{10}(Re_x) ]^{-2.584} </math> |
| - | + | (equation 38 in [[#References|[1]]]): | |
| + | :<math>1.0/C_f^{1/2} = 1.7 + 4.15 \, log_{10} (Re_x \, C_f) </math> | ||
| + | |||
| + | The following skin friction formulas are extracted from [[#References|[2]]],p.19. Proper reference needed: | ||
| + | |||
| + | Prandtl (1927): | ||
| + | :<math> C_f = 0.074 \, Re_x^{-1/5} </math> | ||
| + | |||
| + | Telfer (1927): | ||
| + | :<math> C_f = 0.34 \, Re_x^{-1/3} + 0.0012 </math> | ||
| + | |||
| + | Prandtl-Schlichting (1932): | ||
| + | :<math> C_f = 0.455 \, [ log_{10}(Re_x)]^{-2.58} </math> | ||
| + | |||
| + | Schoenherr (1932): | ||
| + | :<math> C_f = 0.0586 \, [ log_{10}(Re_x \, C_f )]^{-2} </math> | ||
| + | |||
| + | Schultz-Grunov (1940): | ||
| + | :<math> C_f = 0.427 \, [ log_{10}(Re_x) - 0.407]^{-2.64} </math> | ||
| + | |||
| + | Kempf-Karman (1951): | ||
| + | :<math> C_f = 0.055 \, Re_x^{-0.182} </math> | ||
| + | |||
| + | Lap-Troost (1952): | ||
| + | :<math> C_f = 0.0648 \, [log_{10}(Re_x \, C_f^{0.5})-0.9526]^{-2} </math> | ||
| + | |||
| + | Landweber (1953): | ||
| + | :<math> C_f = 0.0816 \, [log_{10}(Re_x) - 1.703]^{-2} </math> | ||
| + | |||
| + | Hughes (1954): | ||
| + | :<math> C_f = 0.067 \, [log_{10}(Re_x) - 2 ] ^{-2} </math> | ||
| + | |||
| + | Wieghard (1955): | ||
| + | :<math> C_f = 0.52 \, [log_{10}(Re_x)] ^{-2.685} </math> | ||
| + | |||
| + | ITTC (1957): | ||
| + | :<math> C_f = 0.075 \, [log_{10}(Re_x) - 2 ] ^{-2} </math> | ||
| + | |||
| + | Gadd (1967): | ||
| + | :<math> C_f = 0.0113 \, [log_{10}(Re_x) - 3.7 ] ^{-1.15} </math> | ||
| + | |||
| + | Granville (1977): | ||
| + | :<math> C_f = 0.0776 \, [log_{10}(Re_x) - 1.88 ] ^{-2} + 60 \, Re_x^{-1} </math> | ||
| + | |||
| + | Date Turnock (1999): | ||
| + | :<math> C_f = [4.06 \, log_{10}(Re_x \, C_f) - 0.729]^{-2} </math> | ||
| + | |||
| + | |||
| + | == References == | ||
| + | # {{reference-paper|author=von Karman, Theodore |year=1934|title=Turbulence and Skin Friction|rest=J. of the Aeronautical Sciences, Vol. 1, No 1, 1934, pp. 1-20}} | ||
| + | # {{reference-paper|author=Lazauskas, Leo Victor |year=2005|title=Hydrodynamics of Advanced High-Speed Sealift Vessels|rest=Master Thesis, University of Adelaide, Australia ([http://digital.library.adelaide.edu.au/dspace/bitstream/2440/37729/1/02whole.pdf download])}} | ||
# {{reference-book|author=Schlichting, Hermann |year=1979|title=Boundary Layer Theory|rest=ISBN 0-07-055334-3, 7th Edition}} | # {{reference-book|author=Schlichting, Hermann |year=1979|title=Boundary Layer Theory|rest=ISBN 0-07-055334-3, 7th Edition}} | ||
| Line 30: | Line 80: | ||
''Someone should add more data about total skin friction approximations, Prandtl-Schlichting skin-friction formula, and the Karman-Schoenherr equation.'' | ''Someone should add more data about total skin friction approximations, Prandtl-Schlichting skin-friction formula, and the Karman-Schoenherr equation.'' | ||
| + | ''Add proper reference for equations in [2]'' | ||
{{stub}} | {{stub}} | ||
| + | |||
| + | Edit: | ||
| + | With regards to the 1/7th power law, in Schlichtings book (see references) the formula describing Cf over a flat plate , without pressure gradient, is Cf=0.0725*Re^(-1/5) and it is valid between 5x10^5<Re<10^7 with the assumption of the flow being turbulent from the leading edge (page 639) | ||
| + | This is found in page 638 , formula 21.11. | ||
| + | |||
| + | Taking into account that the flow is laminar for the first part of the plate and using Blasius's equeation, after providing corrective some corrective factors , Schlichting in page 644 states: | ||
| + | Cf=0.02666*Rl^(-0.139) | ||
| + | There should be a separation between local and total skin friction on the plate.grizos | ||
Latest revision as of 12:14, 14 January 2016
The skin friction coefficient,  , is defined by:
, is defined by:
Where 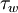 is the local wall shear stress,
is the local wall shear stress, 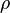 is the fluid density and
is the fluid density and  is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).
is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).
For a turbulent boundary layer several approximation formulas for the local skin friction for a flat plate can be used:
1/7 power law:
1/7 power law with experimental calibration (equation 21.12 in [3]):
Schlichting (equation 21.16 footnote in [3])
Schultz-Grunov (equation 21.19a in [3]):
(equation 38 in [1]):
The following skin friction formulas are extracted from [2],p.19. Proper reference needed:
Prandtl (1927):
Telfer (1927):
Prandtl-Schlichting (1932):
Schoenherr (1932):
Schultz-Grunov (1940):
Kempf-Karman (1951):
Lap-Troost (1952):
Landweber (1953):
Hughes (1954):
Wieghard (1955):
ITTC (1957):
Gadd (1967):
Granville (1977):
Date Turnock (1999):
References
- von Karman, Theodore (1934), "Turbulence and Skin Friction", J. of the Aeronautical Sciences, Vol. 1, No 1, 1934, pp. 1-20.
- Lazauskas, Leo Victor (2005), "Hydrodynamics of Advanced High-Speed Sealift Vessels", Master Thesis, University of Adelaide, Australia (download).
- Schlichting, Hermann (1979), Boundary Layer Theory, ISBN 0-07-055334-3, 7th Edition.
To do
Someone should add more data about total skin friction approximations, Prandtl-Schlichting skin-friction formula, and the Karman-Schoenherr equation. Add proper reference for equations in [2]
Edit:
With regards to the 1/7th power law, in Schlichtings book (see references) the formula describing Cf over a flat plate , without pressure gradient, is Cf=0.0725*Re^(-1/5) and it is valid between 5x10^5<Re<10^7 with the assumption of the flow being turbulent from the leading edge (page 639)
This is found in page 638 , formula 21.11.
Taking into account that the flow is laminar for the first part of the plate and using Blasius's equeation, after providing corrective some corrective factors , Schlichting in page 644 states: Cf=0.02666*Rl^(-0.139) There should be a separation between local and total skin friction on the plate.grizos

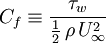
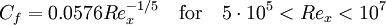
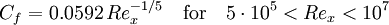
![C_f = [ 2 \, log_{10}(Re_x) - 0.65 ] ^{-2.3} \quad \mbox{for} \quad Re_x < 10^9](/W/images/math/c/a/4/ca4dc895c55260e9f9244eb0465141c8.png)
![C_f = 0.370 \, [ log_{10}(Re_x) ]^{-2.584}](/W/images/math/3/4/4/34492727370cbb6fa12a571f65a1388a.png)
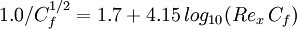
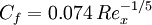

![C_f = 0.455 \, [ log_{10}(Re_x)]^{-2.58}](/W/images/math/5/4/6/5467f64b95b410d418b2e5257ccfa842.png)
![C_f = 0.0586 \, [ log_{10}(Re_x \, C_f )]^{-2}](/W/images/math/0/5/1/0517e14ad72f9e240a9d537681a68a5f.png)
![C_f = 0.427 \, [ log_{10}(Re_x) - 0.407]^{-2.64}](/W/images/math/b/d/0/bd032a44b9b3e0efb177d2095586e673.png)
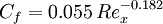
![C_f = 0.0648 \, [log_{10}(Re_x \, C_f^{0.5})-0.9526]^{-2}](/W/images/math/a/0/6/a06720ea4112676a8dfddf461267897c.png)
![C_f = 0.0816 \, [log_{10}(Re_x) - 1.703]^{-2}](/W/images/math/e/3/2/e3275545f39f2589f820703fbf0e68c5.png)
![C_f = 0.067 \, [log_{10}(Re_x) - 2 ] ^{-2}](/W/images/math/b/a/5/ba51e1668f07b0b204e2661190ccab3b.png)
![C_f = 0.52 \, [log_{10}(Re_x)] ^{-2.685}](/W/images/math/4/1/d/41d1dfc26b81ccb5141b86a44dc0e35e.png)
![C_f = 0.075 \, [log_{10}(Re_x) - 2 ] ^{-2}](/W/images/math/2/8/1/281d43a24f91a71bc89512dfd0e1e13c.png)
![C_f = 0.0113 \, [log_{10}(Re_x) - 3.7 ] ^{-1.15}](/W/images/math/9/7/f/97f180fb245f42f56db823a0433fe82a.png)
![C_f = 0.0776 \, [log_{10}(Re_x) - 1.88 ] ^{-2} + 60 \, Re_x^{-1}](/W/images/math/f/8/5/f858769b3aa5a365c535e5bf15745491.png)
![C_f = [4.06 \, log_{10}(Re_x \, C_f) - 0.729]^{-2}](/W/images/math/d/c/3/dc3b85bc6b0d869a9a558363fd876afb.png)