CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > K-epsilon models

K-epsilon models

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
(→Introduction)
(→References)
 
(5 intermediate revisions not shown)
Line 2: Line 2:
== Introduction ==
== Introduction ==
-
The K-epsilon model is one of the most common [[Turbulence modeling|turbulence models]]. It is a [[Two equation models|two equation model]], that means, it includes two extra transport equations to represent the turbulent properties of the flow. This allows a two equation model to account for history effects like convection and diffusion of turbulent energy.
+
The K-epsilon model is one of the most common [[Turbulence modeling|turbulence models]], although it just doesn't perform well in cases of large adverse pressure gradients (Reference 4). It is a [[Two equation models|two equation model]], that means, it includes two extra transport equations to represent the turbulent properties of the flow. This allows a two equation model to account for history effects like convection and diffusion of turbulent energy.
The first transported variable is turbulent kinetic energy, <math>k</math>.  The second transported variable in this case is the turbulent dissipation, <math>\epsilon</math>. It is the variable that determines the scale of the turbulence, whereas the first variable, <math>k</math>, determines the energy in the turbulence.
The first transported variable is turbulent kinetic energy, <math>k</math>.  The second transported variable in this case is the turbulent dissipation, <math>\epsilon</math>. It is the variable that determines the scale of the turbulence, whereas the first variable, <math>k</math>, determines the energy in the turbulence.
-
To define calculate boundary calculations for this model see [[Turbulence free-stream boundary conditions|turbulence free-stream boundary conditions]]
+
There are two major formulations of K-epsilon models (see [[#References|References]] 2 and 3).  That of Launder and Sharma is typically called the [[Standard k-epsilon model | "Standard" K-epsilon Model]].  The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.
 +
 
 +
As described in [[#References|Reference]] 1, the K-epsilon model has been shown to be useful for free-shear layer flows with relatively small pressure gradients.  Similarly, for wall-bounded and internal flows, the model gives good results only in cases where mean pressure gradients are small; accuracy has been shown experimentally to be reduced for flows containing large adverse pressure gradients.  One might infer then, that the K-epsilon model would be an inappropriate choice for problems such as inlets and compressors.
 +
 
 +
To calculate boundary conditions for these models see [[Turbulence free-stream boundary conditions|turbulence free-stream boundary conditions]].
== Usual K-epsilon models ==
== Usual K-epsilon models ==
Line 15: Line 19:
== Miscellaneous ==
== Miscellaneous ==
# [[Near-wall treatment for k-epsilon models]]
# [[Near-wall treatment for k-epsilon models]]
 +
 +
==References==
 +
[1] {{reference-paper|author=Bardina, J.E., Huang, P.G., Coakley, T.J.|year=1997|title=Turbulence Modeling Validation, Testing, and Development|rest=NASA Technical Memorandum 110446}}
 +
 +
[2] {{reference-paper|author=Jones, W. P., and Launder, B. E.|year=1972|title=The Prediction of Laminarization with a Two-Equation Model of
 +
Turbulence|rest= International Journal of Heat and Mass Transfer, vol. 15, 1972, pp. 301-314}}
 +
 +
[3] {{reference-paper|author=Launder, B. E., and Sharma, B. I.|year=1974|title=Application of the Energy Dissipation Model of Turbulence to
 +
the Calculation of Flow Near a Spinning Disc|rest=Letters in Heat and Mass Transfer, vol. 1, no. 2, pp. 131-138}}
 +
 +
[4] '''Wilcox, David C (1998)'''. "Turbulence Modeling for CFD". Second edition. Anaheim: DCW Industries, 1998. pp. 174.
[[Category:Turbulence models]]
[[Category:Turbulence models]]
{{stub}}
{{stub}}

Latest revision as of 16:03, 18 June 2011

Turbulence modeling
Turbulence
RANS-based turbulence models
  1. Linear eddy viscosity models
    1. Algebraic models
      1. Cebeci-Smith model
      2. Baldwin-Lomax model
      3. Johnson-King model
      4. A roughness-dependent model
    2. One equation models
      1. Prandtl's one-equation model
      2. Baldwin-Barth model
      3. Spalart-Allmaras model
    3. Two equation models
      1. k-epsilon models
        1. Standard k-epsilon model
        2. Realisable k-epsilon model
        3. RNG k-epsilon model
        4. Near-wall treatment
      2. k-omega models
        1. Wilcox's k-omega model
        2. Wilcox's modified k-omega model
        3. SST k-omega model
        4. Near-wall treatment
      3. Realisability issues
        1. Kato-Launder modification
        2. Durbin's realizability constraint
        3. Yap correction
        4. Realisability and Schwarz' inequality
  2. Nonlinear eddy viscosity models
    1. Explicit nonlinear constitutive relation
      1. Cubic k-epsilon
      2. EARSM
    2. v2-f models
      1. \overline{\upsilon^2}-f model
      2. \zeta-f model
  3. Reynolds stress model (RSM)
Large eddy simulation (LES)
  1. Smagorinsky-Lilly model
  2. Dynamic subgrid-scale model
  3. RNG-LES model
  4. Wall-adapting local eddy-viscosity (WALE) model
  5. Kinetic energy subgrid-scale model
  6. Near-wall treatment for LES models
Detached eddy simulation (DES)
Direct numerical simulation (DNS)
Turbulence near-wall modeling
Turbulence free-stream boundary conditions
  1. Turbulence intensity
  2. Turbulence length scale

Contents

Introduction

The K-epsilon model is one of the most common turbulence models, although it just doesn't perform well in cases of large adverse pressure gradients (Reference 4). It is a two equation model, that means, it includes two extra transport equations to represent the turbulent properties of the flow. This allows a two equation model to account for history effects like convection and diffusion of turbulent energy.

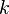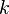The first transported variable is turbulent kinetic energy, k. The second transported variable in this case is the turbulent dissipation, \epsilon. It is the variable that determines the scale of the turbulence, whereas the first variable, k, determines the energy in the turbulence.

There are two major formulations of K-epsilon models (see References 2 and 3). That of Launder and Sharma is typically called the "Standard" K-epsilon Model. The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.

As described in Reference 1, the K-epsilon model has been shown to be useful for free-shear layer flows with relatively small pressure gradients. Similarly, for wall-bounded and internal flows, the model gives good results only in cases where mean pressure gradients are small; accuracy has been shown experimentally to be reduced for flows containing large adverse pressure gradients. One might infer then, that the K-epsilon model would be an inappropriate choice for problems such as inlets and compressors.

To calculate boundary conditions for these models see turbulence free-stream boundary conditions.

Usual K-epsilon models

  1. Standard k-epsilon model
  2. Realisable k-epsilon model
  3. RNG k-epsilon model

Miscellaneous

  1. Near-wall treatment for k-epsilon models

References

[1] Bardina, J.E., Huang, P.G., Coakley, T.J. (1997), "Turbulence Modeling Validation, Testing, and Development", NASA Technical Memorandum 110446.

[2] Jones, W. P., and Launder, B. E. (1972), "The Prediction of Laminarization with a Two-Equation Model of Turbulence", International Journal of Heat and Mass Transfer, vol. 15, 1972, pp. 301-314.

[3] Launder, B. E., and Sharma, B. I. (1974), "Application of the Energy Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc", Letters in Heat and Mass Transfer, vol. 1, no. 2, pp. 131-138.

[4] Wilcox, David C (1998). "Turbulence Modeling for CFD". Second edition. Anaheim: DCW Industries, 1998. pp. 174.


This article is a stub, a short article which needs to be improved. You can help by expanding it.
Retrieved from "https://mail.cfd-online.com/Wiki/K-epsilon_models"
My wiki