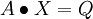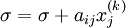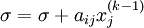Gauss-Seidel method
From CFD-Wiki
(Difference between revisions)
| Line 6: | Line 6: | ||
In matrix terms, the definition of the Gauss-Seidel method can be expressed as : <br> | In matrix terms, the definition of the Gauss-Seidel method can be expressed as : <br> | ||
<math> | <math> | ||
| - | x^{(k)} = \left( {D - L} \right)^{ - 1} \left( {Ux^{(k - 1)} + | + | x^{(k)} = \left( {D - L} \right)^{ - 1} \left( {Ux^{(k - 1)} + q} \right) |
</math><br> | </math><br> | ||
Where '''D''','''L''' and '''U''' represent the diagonal, lower triangular and upper triangular matrices of coefficient matrix '''A''' and k is iteration counter.<br> | Where '''D''','''L''' and '''U''' represent the diagonal, lower triangular and upper triangular matrices of coefficient matrix '''A''' and k is iteration counter.<br> | ||
| Line 29: | Line 29: | ||
: end (k-loop) | : end (k-loop) | ||
---- | ---- | ||
| + | |||
| + | |||
| + | ---- | ||
| + | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Revision as of 06:23, 3 October 2005
We seek the solution to set of linear equations:
For the given matrix A and vectors X and Q.
In matrix terms, the definition of the Gauss-Seidel method can be expressed as :
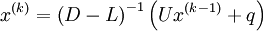
Where D,L and U represent the diagonal, lower triangular and upper triangular matrices of coefficient matrix A and k is iteration counter.
The pseudocode for the Gauss-Seidel algorithm:
Algorithm
- Chose an intital guess
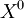to the solution
- for k := 1 step 1 untill convergence do
- for i := 1 step until n do
-
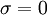
- for j := 1 step until i-1 do
-
- end (j-loop)
- for j := i+1 step until n do
-
- end (j-loop)
-
-
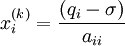
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (k-loop)
Return to Numerical Methods
