Combustion
From CFD-Wiki
(→Governing Equations) |
(→Eddy Break-Up model: first edit) |
||
| Line 93: | Line 93: | ||
==== Eddy Break-Up model ==== | ==== Eddy Break-Up model ==== | ||
| + | |||
| + | The Eddy Break-Up model is the typical example of mixed-is-burnt combustion model. | ||
| + | It is based on the work of Magnussen and Hjertager, | ||
| + | and Spalding and can be found in all CFD packages. | ||
| + | The model assumes the reactions to be completed in the moment of mixing, so that the reaction rate is completely controlled by turbulent mixing. | ||
| + | The combustion is described by a single step global chemical reaction: | ||
| + | |||
| + | <table width="100%"> | ||
| + | <tr><td> | ||
| + | :<math> | ||
| + | F + \nu_s O \rightarrow (1+\nu_s) P | ||
| + | </math></td><td width="5%"></td></tr></table> | ||
| + | |||
| + | in which <b>F</b> stands for fuel, <b>O</b> for oxidiser and <b>P</b> for products of the reaction. Alternativelly we can have multistep scheme, where each reaction has its own mean reaction rate. | ||
| + | The mean reaction rate is given by: | ||
| + | |||
| + | <table width="100%"> | ||
| + | <tr><td> | ||
| + | :<math> | ||
| + | \bar{\dot\omega}_F=A_{EB} \frac{\varepsilon}{k} | ||
| + | min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu}, | ||
| + | B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right] | ||
| + | </math></td><td width="5%"></td></tr></table> | ||
| + | |||
| + | |||
| + | <math>\bar{C}</math> denotes mean concentrations for fuel, oxidiser and products | ||
| + | respectively, <b>A</b> and <b>B</b> are model constants with typical values of 0.5 | ||
| + | and 4.0 respectively. The values of these constants are fitted according | ||
| + | to the experimental results and they are suitable for most of the general cases. | ||
| + | Still they are just constants based on experimental fitting and they need not | ||
| + | be suitable for <b>all</b> the situations. | ||
| + | Care must be taken especially in highly strained regions, where the ratio of <math>k</math> | ||
| + | to <math>\varepsilon</math> is large (flame-holder wakes, walls ...). In those regions a positive reaction rate occurs and an artificial flame can be observed. | ||
| + | CFD codes usually has some remedies to overcome this problem. | ||
| + | |||
| + | This model largely over-predicts temperatures and concentrations of species like <i>CO</i> and other species. Still this model is quite popular for its simplicity and relatively easy convergence and implementation. | ||
==== Bray-Moss-Libby Model ==== | ==== Bray-Moss-Libby Model ==== | ||
Revision as of 14:01, 2 October 2005
Contents |
What is combustion -- Physics versus modelling
Combustion phenomena consists of many physical and chemical processes with broad range of time scales. Mathematical description of combustion is not always trivial. Analytical solutions exists only for basic situations of laminar flame and because of its assumptions it is often restricted to few problems solved usually in zero or one-dimensional space.
Problems solved today concern mainly turbulent flows, gas as well as liquid fuels, pollution issues (products of combustion as well as for example noise pollution). These problems require not only extensive experimental work, but also numerical modelling. All combustion models must be validated against the experiments as each one has its own drawbacks and limits. However here the modelling part will be mainly addressed.
Reaction mechanisms
The combustion is mainly chemical process and although we can, to some extend, describe flame without any chemistry informations, for modelling of flame propagation we need to know the speed of reactions, product concentrations, temperature and other parameters. Therefore more or less detailed information about reaction kinetics is essential for any combustion model. Mixture will generally combust, if the reaction of fuel and oxidiser is fast enough to maintain until all of the mixture is burned into products. If the reaction is too slow, the flame will extinguish, if too fast, explosion or even detonation will occur. The reaction rate of typical combustion reaction is influenced mainly by concentration of reactants, temperature and pressure.
A stoichiometric equation of an arbitrary equation can be written as:
|
|
where $\nu$ is the stoichiometric coefficient, 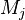 is arbitrary species. One
prime specifies the reactants and double prime products of the reaction.
is arbitrary species. One
prime specifies the reactants and double prime products of the reaction.
Reaction rate, expressing the rate of disappearance of reactant i of such a reaction, is defined as:
|
|
in which k is the specific reaction rate constant. Arrhenius found that this constant is a function only of temperature and this function is defined as:
|
|
where A is pre--exponential factor, E is activation energy and 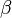 is
temperature exponent.
These constants for given reactions can be found in literature.
The reaction mechanism can be given from experiments for every reaction
resolved, it could be also constructed numerically by automatic generation
method (see [Griffiths (1994)] for review on reaction mechanisms).
For simple hydrocarbon tens to hundreds of reactions are involved.
By analysis and systematic reduction of reaction mechanisms global reaction
(from one to five step reactions) can be found (see [Westbrook (1984)]).
is
temperature exponent.
These constants for given reactions can be found in literature.
The reaction mechanism can be given from experiments for every reaction
resolved, it could be also constructed numerically by automatic generation
method (see [Griffiths (1994)] for review on reaction mechanisms).
For simple hydrocarbon tens to hundreds of reactions are involved.
By analysis and systematic reduction of reaction mechanisms global reaction
(from one to five step reactions) can be found (see [Westbrook (1984)]).
Governing Equations
The mass fraction transport equation for k-th species 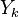
| (1) | </tr>
where Ficks law is assumed for scalar diffusion and
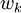 is the species reaction rate.
is the species reaction rate.
Infinitely fast chemistry
Premixed Combustion
Turbulent flame speed model
Eddy Break-Up model
The Eddy Break-Up model is the typical example of mixed-is-burnt combustion model. It is based on the work of Magnussen and Hjertager, and Spalding and can be found in all CFD packages. The model assumes the reactions to be completed in the moment of mixing, so that the reaction rate is completely controlled by turbulent mixing. The combustion is described by a single step global chemical reaction:
|
|
in which F stands for fuel, O for oxidiser and P for products of the reaction. Alternativelly we can have multistep scheme, where each reaction has its own mean reaction rate. The mean reaction rate is given by:
|
|
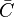 denotes mean concentrations for fuel, oxidiser and products
respectively, A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to the experimental results and they are suitable for most of the general cases.
Still they are just constants based on experimental fitting and they need not
be suitable for all the situations.
Care must be taken especially in highly strained regions, where the ratio of
denotes mean concentrations for fuel, oxidiser and products
respectively, A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to the experimental results and they are suitable for most of the general cases.
Still they are just constants based on experimental fitting and they need not
be suitable for all the situations.
Care must be taken especially in highly strained regions, where the ratio of 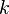 to
to  is large (flame-holder wakes, walls ...). In those regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually has some remedies to overcome this problem.
is large (flame-holder wakes, walls ...). In those regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually has some remedies to overcome this problem.
This model largely over-predicts temperatures and concentrations of species like CO and other species. Still this model is quite popular for its simplicity and relatively easy convergence and implementation.
Bray-Moss-Libby Model
Non premixed combustion
Conserved scalar equilibrium models
Finite rate chemistry
Premixed Combustion
Coherent Flame Model
Flamelets based on G equation
Non-premixed Combustion
Flamelets based on conserved scalar
Conditional Moment Closure (CMC)
Multiple Mapping Closure (MMC)
Linear Eddy Model
PDF transport models
Lagrangian
Eulerian
References
- Griffiths J.F. (1994), "Reduced Kinetic Models and Their Application to Practical Combustion Systems", Prog. in Energy and Combustion Science,Vol. 21, pp. 25-107.
- Westbrook, Ch.K., Dryer,F.L., (1984), "Chemical Kinetic Modeling of Hydrocarbon Combustion", Prog. in Energy and Combustion Science,Vol. 10, pp. 1-57.

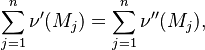
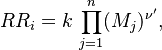
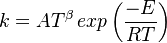

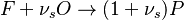
![\bar{\dot\omega}_F=A_{EB} \frac{\varepsilon}{k}
min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu},
B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right]](/W/images/math/6/b/7/6b7935410fbd22690d4f017ef7cb42c4.png)