Other Schemes (unclassified) - structured grids
From CFD-Wiki
(→CLAM - Curved-Line Advection Method) |
(→CLAM - Curved-Line Advection Method) |
||
| Line 317: | Line 317: | ||
identical to HLPA | identical to HLPA | ||
| + | |||
| + | normalised variables - uniform grids | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | \hat{\phi_{f}}= | ||
| + | \begin{cases} | ||
| + | \hat{\phi_{C}} \left( 2 - \hat{\phi_{C}} \right) \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq 1 \\ | ||
| + | \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | </td><td width="5%">(2)</td></tr></table> | ||
| + | |||
| + | normalised variables - non-uniform grids (NVSF - compare with HLPA - here is used another variant of notation) | ||
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
| Line 322: | Line 336: | ||
\hat{\phi}_{f} = | \hat{\phi}_{f} = | ||
\begin{cases} | \begin{cases} | ||
| - | \hat{\phi}_{C} | + | \frac{\hat{\xi}_f - \hat{\xi}^{2}_{C}}{\hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C - \frac{\hat{\xi}_f - \hat{\xi}_{C}}{\hat{\xi}_C \left( 1 - \hat{\xi}_C \right)}\hat{\phi}^{2}_{C} & 0 \leq \hat{\phi}_{C} \leq 1 \\ |
| + | \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
Revision as of 22:45, 8 November 2005
Chakravarthy-Osher limiter
Sweby 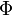 - limiter
- limiter
Superbee limiter
R-k limiter
MINMOD - MINimum MODulus
Harten A. High resolution schemes using flux limiters for hyperbolic conservation laws. Journal of Computational Physics 1983; 49: 357-393
A. Harten
High Resolution Schemes for Hyperbolic Conservation Laws
J. Comp. Phys., vol. 49, no. 3, pp. 225-232, 1991
Identical to SOUCUP
Normalized variables - uniform grids
|
| (2) |
Normalized variables - non-uniform grids (NVSF)
|
| (2) |
SOUCUP - Second-Order Upwind Central differnce-first order UPwind
Zhu J. (1992), "On the higher-order bounded discretization schemes for finite volume computations of incompressible flows", Computational Methods in Applied Mechanics and Engineering. 98. 345-360.
J. Zhu, W.Rodi (1991), "A low dispersion and bounded convection scheme", Comp. Meth. Appl. Mech.&Engng, Vol. 92, p 225.
Normalized variables - uniform grids
|
| (2) |
Normalized variables - non-uniform grids
|
| (2) |
where
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
ISNAS - Interpolation Scheme which is Nonoscillatory for Advected Scalars
Third-order flux-limiter scheme
M. Zijlema , On the construction of a third-order accurate monotone convection scheme with application to turbulent flows in general domains. International Journal for numerical methods in fluids, 22:619-641, 1996.
COPLA - COmbination of Piecewise Linear Approximation
Seok Ki Choi, Ho Yun Nam, Mann Cho
Evaluation of a High-Order Bounded Convection Scheme: Three-Dimensional Numerical Experiments
Numerical Heat Transfer, Part B, 28:23-38, 1995
|
| (2) |
where
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
and
|
| (1) |
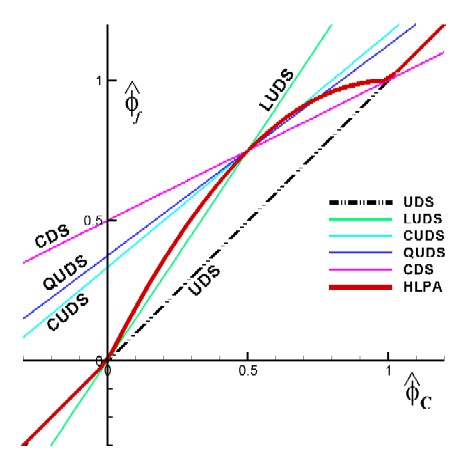
HLPA - Hybrid Linear / Parabolic Approximation
Zhu J. Low Diffusive and oscillation-free convection scheme // Communications and Applied Numerical Methods. 1991. 7, N3. 225-232.
Zhu J., Rodi W. A low dispersion and bounded discretization schemes for finite volume computations of incompressible flows // Computational Methods for Applied Mechanics and Engineering. 1991. 92. 87-96
In this scheme, the normalized face value is approximated by a combination of linear and parabolic charachteristics passing through the points, O, Q, and P in the NVD. It satisfies TVD condition and is second-order accurate
Usual variables
|
| (2) |
Normalized variables - uniform grids
|
| (2) |
Normalized variables - non-uniform grids
|
| (2) |
where
|
| (2) |
|
| (2) |
|
| (2) |
Implementation
Using the switch factors:
for 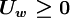
|
| (2) |
for 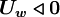
|
| (2) |
and taken all the possible flow directions into account, the un-normalized form of equation can be written as
|
| (2) |
where
|
| (2) |
|
| (2) |
LODA - Local Oscillation-Damping Algorithm
J. Zhu and M.A. Leschziner
A local oscillation-damping algorithm for higher-order convection schemes
Comput. Methods Appl. Mech. Engnrng 67 (1988) 355-366
CLAM - Curved-Line Advection Method
Van Leer B. , Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. Journal of Computational Physics 1974; 14:361-370
identical to HLPA
normalised variables - uniform grids
|
| (2) |
normalised variables - non-uniform grids (NVSF - compare with HLPA - here is used another variant of notation)
|
| (2) |
van Leer harmonic
BSOU
G. Papadakis, G. Bergeles.
A locally modified second order upwind scheme for convection terms discretization.
Int. J. Numer. Meth. Heat Fluid Flow, 5.49-62, 1995
MSOU - Monotonic Second Order Upwind Differencing Scheme
Sweby
Koren
bounded CUS
B. Koren
A robust upwind discretisation method for advection, diffusion and source terms
In: Numerical Mthods for Advection-Diffusion Problems, Ed. C.B.Vreugdenhil& B.Koren, Vieweg, Braunscheweigh, p.117, (1993)
H-CUS
bounded CUS
N.P.Waterson H.Deconinck
A unified approach to the design and application of bounded high-order convection schemes
VKI-preprint, 1995-21, (1995)
MLU
B. Noll
Evaluation of a bounded high-resolution scheme for combustor flow computations
AIAA J., vol. 30, No. 1, p.64 (1992)
LPPA - Linear and Piecewise / Parabolic Approximasion
Normalized variables - uniform grids
|
| (2) |
Normalized variables - non-uniform grids
|
| (2) |
where
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
|
| (2) |
GAMMA
Jasak H., Weller H.G., Gosman A.D.
High resolution NVD differencing scheme for arbitrarily unstructured meshes
International Journal for Numerical Methods in Fluids
1999, 31: 431-449
|
| (2) |
|
| (2) |
CUBISTA - Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection
M.A. Alves, P.J.Oliveira, F.T. Pinho, A convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection // International Lournal For Numerical Methods in Fluids 2003, 41; 47-75
normalised variables - uniform grid
|
| (2) |
normalised variables - non-uniform grid (NVSF)
|
| (2) |
Return to Numerical Methods
Return to Approximation Schemes for convective term - structured grids

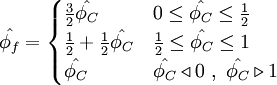
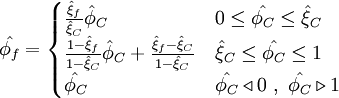

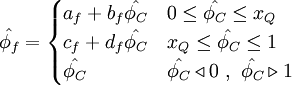
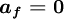


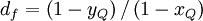
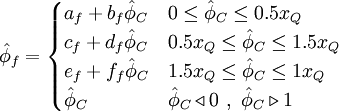
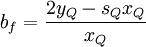
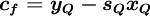
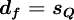

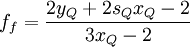
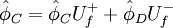
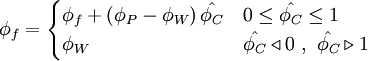
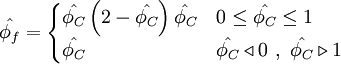
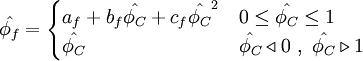
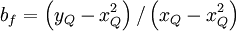
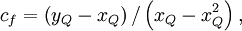
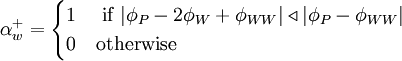
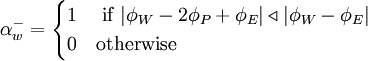
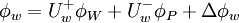
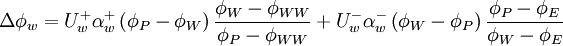
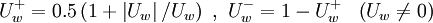
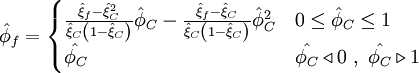
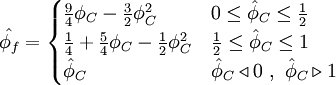
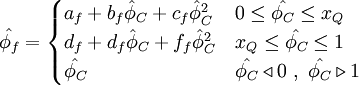
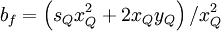
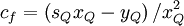
![d_{f} = \left[ x^{2}_{Q} + s_{Q} \left( x^{2}_{Q} - x_{Q} \right)+ \left( 1 - 2 x_{Q} \right) \right] / \left( 1 - x_{Q} \right)^{2}](/W/images/math/c/f/3/cf3a8ae5368140d73bbd0e47679c3d75.png)
![e_{f} = \left[ -2 x_{Q} + s_{Q} \left( 1 - x^{2}_{Q} \right) + 2 x_{Q} y_{Q} \right] / \left( 1 - x_{Q} \right)^{2}](/W/images/math/1/5/8/158987c952653a445307981f1ce1df34.png)
![f_{f} = \left[ 1 + s_{Q} \left( x_{Q} - 1 \right) - 2 y_{Q} \right] / \left( 1 - x_{Q} \right)^{2}](/W/images/math/b/6/d/b6d3b9aac2cbccd793ab742b82ec5ced.png)
![\hat{\phi}_{f}=
\begin{cases}
\hat{\phi}_C \left[ 1 + \frac{1}{2 \beta_m } \left( 1 - \hat{\phi}_C \right) \right] & 0 \triangleleft \hat{\phi}_C \triangleleft \beta_m \\
\frac{1}{2}\hat{\phi}_{C} + \frac{1}{2} & \beta_m \leq \hat{\phi}_C \leq 1 \\
\hat{\phi}_C & \mbox{elsewhere}
\end{cases}](/W/images/math/2/f/5/2f532adb442b5befda220c9446f1f126.png)
![\hat{\phi}_{f}=
\begin{cases}
\hat{\phi}_C \left[1 + \frac{1}{\beta_m} \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } \left( 1 - \hat{\phi}_C \right) \right] & 0 \triangleleft \hat{\phi}_C \triangleleft \beta_m \\
\frac{ 1 - \hat{\xi}_f }{ 1 - \hat{\xi}_C } \hat{\phi}_C + \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } & \beta_m \leq \hat{\phi}_C \leq 1 \\
\hat{\phi}_C & \mbox{elsewhere}
\end{cases}](/W/images/math/9/0/4/904591fcfdb8b511241c15ea1b63ec46.png)
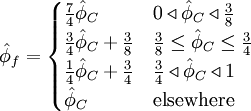
![\hat{\phi}_{f}=
\begin{cases}
\left[1+\frac{\hat{\xi}_f- \hat{\xi}_C}{3\left( 1 - \hat{\xi}_C \right) } \right] \frac{\hat{\xi}_f}{\hat{\xi}_C} \hat{\phi}_C & 0 \triangleleft \hat{\phi}_C \triangleleft \frac{3}{4}\hat{\xi}_C \\
\frac{\hat{\xi}_f \left(1- \hat{\xi}_f \right)}{ \hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C + \frac{\hat{\xi}_f \left( \hat{\xi}_f - \hat{\xi}_C \right)}{1- \hat{\xi}_C} & \frac{3}{4} \hat{\xi}_C \leq \hat{\phi}_C \leq \frac{1 + 2 \left( \hat{\xi}_f - \hat{\xi}_C \right) }{ 2 \hat{\xi}_f - \hat{\xi}_C } \hat{\xi}_C \\
\frac{\hat{\xi}_f \left(1- \hat{\xi}_f \right)}{ \hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C + \frac{\hat{\xi}_f \left( \hat{\xi}_f - \hat{\xi}_C \right)}{1- \hat{\xi}_C} & \frac{1 + 2 \left( \hat{\xi}_f - \hat{\xi}_C \right) }{ 2 \hat{\xi}_f - \hat{\xi}_C } \hat{\xi}_C \triangleleft \hat{\phi}_C \triangleleft 1 \\
\hat{\phi}_C & \mbox{elsewhere}
\end{cases}](/W/images/math/a/b/4/ab46002b8a048baa9040b7ae52bd8c64.png)