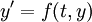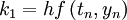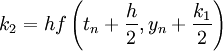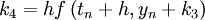Runge Kutta methods
From CFD-Wiki
Discoganya (Talk | contribs) |
Discoganya (Talk | contribs) |
||
| Line 16: | Line 16: | ||
==Algorithm== | ==Algorithm== | ||
| - | ::<math> | + | ::<math>y^\prime = f\left( {t,y} \right) </math> |
| - | ::<math>k_1 = hf\left( { | + | ::<math>k_1 = hf\left( {t_n ,y_n } \right) </math> |
| - | ::<math>k_2 = hf\left( { | + | ::<math>k_2 = hf\left( {t_n + {h \over 2},y_n + {{k_1 } \over 2}} \right) </math> |
| - | ::<math>k_3 = hf\left( { | + | ::<math>k_3 = hf\left( {t_n + {h \over 2},y_n + {{k_2 } \over 2}} \right) </math> |
| - | ::<math>k_4 = hf\left( { | + | ::<math>k_4 = hf\left( {t_n + h,y_n + k_3 } \right) </math> |
::<math>y_{n + 1} = y_n + {{k_1 } \over 6} + {{k_2 } \over 3} + {{k_3 } \over 3} + {{k_4 } \over 6} </math> | ::<math>y_{n + 1} = y_n + {{k_1 } \over 6} + {{k_2 } \over 3} + {{k_3 } \over 3} + {{k_4 } \over 6} </math> | ||
Revision as of 18:29, 23 November 2005
Runge Kutta (RK) methods are an important class of methods for integrating initial value problems formed by ODEs. Runge Kutta methods encompass a wide selection of numerical methods and some commonly used methods such as Explicit or Implicit Euler's Method, the implicit midpoint rule and the trapezoidal rule are actually simplified versions of a general RK method.
For the ODE,
the basic idea is to build a series of "stages", 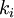 that approximate the solution
that approximate the solution 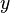 at various points using samples of
at various points using samples of 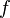 from other stages. Finally, the numerical solution
from other stages. Finally, the numerical solution 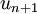 is constructed from a linear combination of
is constructed from a linear combination of 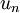 and all the precomputed stages.
and all the precomputed stages.
Since the computation of one stage may involve other stages 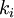 the right hand side
the right hand side 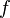 is evaluated in a complicated nonlinear way. The most famous classical RK scheme is described below.
is evaluated in a complicated nonlinear way. The most famous classical RK scheme is described below.
Fourth order Runge-Kutta method
The fourth order Runge-Kutta method could be summarized as:
Algorithm
Return to Numerical Methods