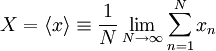Introduction to turbulence/Statistical analysis
From CFD-Wiki
(→1 Foreword) |
(→2 The ensemble and ensemble average) |
||
| Line 12: | Line 12: | ||
==2 The ensemble and ensemble average == | ==2 The ensemble and ensemble average == | ||
| - | + | \section{The mean or ensemble average } | |
| + | |||
| + | |||
| + | The concept of an \textit{ ensebmble average} is based upon the existence of independent statistical event. For example, consider a number of inviduals who are simultaneously flipping unbiased coins. If a value of one is assigned to a head and the value of zero to a tail, then the average of the numbers generated is defined as | ||
| + | |||
| + | |||
| + | \begin{equation} | ||
| + | X_{N}=\frac{1}{N} \sum{x_{n}} | ||
| + | \end{equation} | ||
| + | |||
| + | where our $n$th flip is denoted as $x_{n}$ and $N$ is the total number of flips. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Now if all the coins are the same, it doesn't really matter whether we flip one coin $N$ times, or $N$ coins a single time. The key is that they must all be \textit{independent events} - meaning the probability of achieving a head or tail in a given flip must be completely independent of what happens in all the other flips. Obviously we can't just flip one coin and count it $N$ times; these cleary would not be independent events | ||
| + | |||
| + | Unless you had a very unusual experimental result, you probably noticed that the value of the $X_{10}$'s was also a random variable and differed from ensemble to ensemble. Also the greater the number of flips in the ensemle, thecloser you got to $X_{N}=1/2$. Obviously the bigger $N$, the less fluctuation there is in $X_{N}$ | ||
| + | |||
| + | Now imagine that we are trying to establish the nature of a random variable $x$. The $n$th \textit{realization} of $x$ is denoted as $x_{n}$. The \textit{ensemble average} of $x$ is denoted as $X$ (or $ \left\langle x \right\rangle $ ), and \textit{is defined as} | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | |||
| + | X = \left\langle x \right\rangle \equiv \frac{1}{N} \lim_{N \rightarrow \infty} \sum^{N}_{n=1} x_{n} | ||
| + | |||
| + | </math> | ||
| + | </td><td width="5%">(2)</td></tr></table> | ||
Revision as of 10:09, 16 May 2006
1 Foreword
Much of the study of turbulence requires statistics and stochastic processes, simply because the instanteous motions are too complicated to understand. This should not be taken to mean that the govering equations (usually the Navier-Stokes equations) are stochastic. Even simple non-linear equations can have deterministic solutions that look random. In other words, even though the solutions for a given set of initial and boundary conditions can be perfectly repeatable and predictable at a given time and point in space, it may be impossible to guess from the information at one point or time how it will behave at another (at least without solving the equations). Moreover, a slight change in the intial or boundary conditions may cause large changes in the solution at a given time and location; in particular, changes that we could not have anticipated.
Here will be introduced the simple idea of the ensemble average
Most of the statistical analyses of turbulent flows are based on the idea of an ensemble average in one form or another. In some ways this is rather inconvenient, since it will be obvious from the definitions that it is impossible to ever really measure such a quantity. Therefore we will spendlast part of this chapter talking about how the kind of averages we can compute from data correspond to the hypotetical ensemble average we wish we could have measured. In later chapters we shall introduce more statistical concepts as we require them. But the concepts of this chapter will be all we need to begin a discussion of the averaged equations of motion in Chapter 3
2 The ensemble and ensemble average
\section{The mean or ensemble average }
The concept of an \textit{ ensebmble average} is based upon the existence of independent statistical event. For example, consider a number of inviduals who are simultaneously flipping unbiased coins. If a value of one is assigned to a head and the value of zero to a tail, then the average of the numbers generated is defined as
\begin{equation} X_{N}=\frac{1}{N} \sum{x_{n}} \end{equation}
where our $n$th flip is denoted as $x_{n}$ and $N$ is the total number of flips.
Now if all the coins are the same, it doesn't really matter whether we flip one coin $N$ times, or $N$ coins a single time. The key is that they must all be \textit{independent events} - meaning the probability of achieving a head or tail in a given flip must be completely independent of what happens in all the other flips. Obviously we can't just flip one coin and count it $N$ times; these cleary would not be independent events
Unless you had a very unusual experimental result, you probably noticed that the value of the $X_{10}$'s was also a random variable and differed from ensemble to ensemble. Also the greater the number of flips in the ensemle, thecloser you got to $X_{N}=1/2$. Obviously the bigger $N$, the less fluctuation there is in $X_{N}$
Now imagine that we are trying to establish the nature of a random variable $x$. The $n$th \textit{realization} of $x$ is denoted as $x_{n}$. The \textit{ensemble average} of $x$ is denoted as $X$ (or $ \left\langle x \right\rangle $ ), and \textit{is defined as}
|
| (2) |