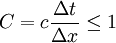Courant–Friedrichs–Lewy condition
From CFD-Wiki
(Difference between revisions)
| Line 11: | Line 11: | ||
where C is called the ''Courant number'' | where C is called the ''Courant number'' | ||
| + | where the [[dimensionless number]] is called the '''Courant number''', | ||
| + | |||
| + | *<math>u</math> is the velocity (whose [[Dimensional analysis#Definition|dimension]] is Length/Time) | ||
| + | *<math>\Delta t</math> is the time step (whose [[Dimensional analysis#Definition|dimension]] is Time) | ||
| + | *<math>\Delta x</math> is the length interval (whose [[Dimensional analysis#Definition|dimension]] is Length). | ||
| + | |||
| + | The value of <math>C_{max}</math> changes with the method used to solve the discretised equation. If an explicit (time-marching) solver is used then typically <math>C_{max} = 1</math>. Implicit (matrix) solvers are usually less sensitive to numerical instability and so larger values of <math>C_{max}</math> may be tolerated. | ||
{{reference-paper | author=Courant, R., K. O. Fredrichs, and H. Lewy | year=1928 | title=Uber die Differenzengleichungen der Mathematischen Physik | rest=Math. Ann, vol.100, p.32, 1928}} | {{reference-paper | author=Courant, R., K. O. Fredrichs, and H. Lewy | year=1928 | title=Uber die Differenzengleichungen der Mathematischen Physik | rest=Math. Ann, vol.100, p.32, 1928}} | ||
{{reference-paper | author=Anderson, Lohn David | year=1995 | title=Computational fluid dynamics: the basics with applications | rest=McGraw-Hill, Inc}} | {{reference-paper | author=Anderson, Lohn David | year=1995 | title=Computational fluid dynamics: the basics with applications | rest=McGraw-Hill, Inc}} | ||
Revision as of 11:49, 26 August 2012
It is an important stability criterion for hyperbolic equations.
In common case it's written as
|
| (2) |
where C is called the Courant number
where the dimensionless number is called the Courant number,
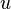is the velocity (whose dimension is Length/Time)
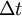is the time step (whose dimension is Time)
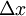is the length interval (whose dimension is Length).
The value of 
changes with the method used to solve the discretised equation. If an explicit (time-marching) solver is used then typically 
. Implicit (matrix) solvers are usually less sensitive to numerical instability and so larger values of may be tolerated.
Courant, R., K. O. Fredrichs, and H. Lewy (1928), "Uber die Differenzengleichungen der Mathematischen Physik", Math. Ann, vol.100, p.32, 1928.
Anderson, Lohn David (1995), "Computational fluid dynamics: the basics with applications", McGraw-Hill, Inc.
