Finite volume
From CFD-Wiki
(Difference between revisions)
m |
(→Basic Equations of CFD) |
||
| Line 17: | Line 17: | ||
Equation (1) is integrated over a control volume and the following discretised equation for <math>\boldsymbol{\phi}</math> is produced: | Equation (1) is integrated over a control volume and the following discretised equation for <math>\boldsymbol{\phi}</math> is produced: | ||
| + | |||
| + | <table width="100%"><tr><td> | ||
| + | :<math> | ||
| + | J_{h}- J_{l} + J_{n}- J_{s} + J_{e}- J_{w} + D_{h} - D_{l} + D_{n} - D_{s} + D_{e} - D_{s} = S_{p} | ||
| + | </math> | ||
| + | </td><td width="5%">(2)</td></tr></table> | ||
Revision as of 22:13, 13 September 2005
Discretisation Schemes for convective terms in General Transport Equation. Finite-Volume Formulation, structured grids
Introduction
Here is describing the discretization schemes of the convective terms in the finite-volume equations. The accuracy, numerical stability and the boundness of the solution depends on the numerical scheme used for these terms. The central issue is the specification of an appropriate relationship between the convected variable, stored at the cell centre and its value at each of the cell faces.
Basic Equations of CFD
All the conservation equations can be written in the same generic differential form:
|
| (1) |
Equation (1) is integrated over a control volume and the following discretised equation for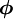 
is produced:
|
| (2) |
