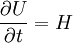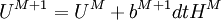Wave propagation
From CFD-Wiki
(Difference between revisions)
| Line 3: | Line 3: | ||
== Compact scheme == | == Compact scheme == | ||
| - | == Runga Kutta == | + | == Runga Kutta == |
Consider | Consider | ||
:<math> \frac {\partial U}{\partial t}=H </math> | :<math> \frac {\partial U}{\partial t}=H </math> | ||
| + | The low storage scheme is implemented as follows | ||
| + | :<math> U^{M+1}=U^M+b^{M+1}dtH^M </math> | ||
| + | |||
== Sample result == | == Sample result == | ||
[[Image:wp_result.jpg]] | [[Image:wp_result.jpg]] | ||
Revision as of 15:47, 19 September 2005
Contents |
Introduction
The 1-D wave propagation problem is used as a test case for studying the dissipation and dispersion errors in a given finite difference scheme.There are a number of schemes which can be used to solve the problem. The usage of a higher order compact stencil with a low storage 4th order Runga Kutta scheme to solve the current problem is discussed.
Compact scheme
Runga Kutta
Consider
The low storage scheme is implemented as follows
Sample result
Reference
Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.
Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.