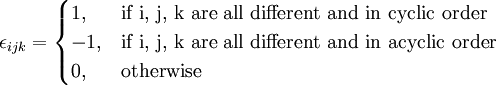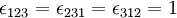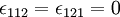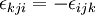Alternating tensor
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| + | The alternating tensor, also known as '''Levi-Civita''' symbol is defined by | ||
| + | |||
:<math> | :<math> | ||
\epsilon_{ijk} = \begin{cases} | \epsilon_{ijk} = \begin{cases} | ||
| Line 5: | Line 7: | ||
0, & \mbox{otherwise} | 0, & \mbox{otherwise} | ||
\end{cases} | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Thus | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{123} = \epsilon_{231} = \epsilon_{312} = 1 | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{321} = \epsilon_{132} = \epsilon_{213} = -1 | ||
| + | </math> | ||
| + | |||
| + | If any index is repeated then the value is zero, e.g., | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{112} = \epsilon_{121} = 0 | ||
| + | </math> | ||
| + | |||
| + | If any two indices are interchanged then the sign changes, e.g., | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{kji} = -\epsilon_{ijk} | ||
</math> | </math> | ||
Revision as of 04:35, 20 September 2005
The alternating tensor, also known as Levi-Civita symbol is defined by
Thus
If any index is repeated then the value is zero, e.g.,
If any two indices are interchanged then the sign changes, e.g.,