Wilcox's k-omega model

From CFD-Wiki

(Difference between revisions)

Revision as of 10:29, 26 September 2005

Kinematic Eddy Viscosity

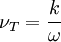
$\nu _T = {k \over \omega }$

Turbulence Kinetic Energy

${{\partial k} \over {\partial t}} + U_j {{\partial k} \over {\partial x_j }} = \tau _{ij} {{\partial U_i } \over {\partial x_j }} - \beta ^* k\omega + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma ^* \nu _T } \right){{\partial k} \over {\partial x_j }}} \right]$

Specific Dissipation Rate

${{\partial \omega } \over {\partial t}} + U_j {{\partial \omega } \over {\partial x_j }} = \alpha {\omega \over k}\tau _{ij} {{\partial U_i } \over {\partial x_j }} - \beta \omega ^2 + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma \nu _T } \right){{\partial \omega } \over {\partial x_j }}} \right]$

Closure Coefficients and Auxilary Relations

$\alpha = {{13} \over {25}}$

$\beta = \beta _0 f_\beta$

$\beta ^* = \beta _0^* f_{\beta ^* }$

$\sigma = {1 \over 2}$

$\sigma ^* = {1 \over 2}$

$\beta _0 = {9 \over {125}}$

$f_\beta = {{1 + 70\chi _\omega } \over {1 + 80\chi _\omega }}$

$f_{\beta ^* } = \left\{ \begin{matrix} {1,} & {\chi _k \le 0} \\ {{{1 + 680\chi _k^2 } \over {1 + 80\chi _k^2 }},} & {\chi _k > 0} \\ \end{matrix} \right.$

Wilcox's k-omega model

From CFD-Wiki

Revision as of 10:29, 26 September 2005

Contents

Kinematic Eddy Viscosity

Turbulence Kinetic Energy

Specific Dissipation Rate

Closure Coefficients and Auxilary Relations

Views

My wiki

wiki navigation

wiki search

wiki toolbox

@@ Line 35: / Line 35: @@
 :<math>
-\alpha  = {{13} \over {25}}
+f_\beta   = {{1 + 70\chi _\omega  } \over {1 + 80\chi _\omega  }}
 </math>