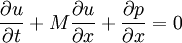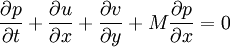2-D linearised Euler equation
From CFD-Wiki
(Difference between revisions)
| Line 4: | Line 4: | ||
:<math> \frac{\partial p}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial p}{\partial x}=0 </math> | :<math> \frac{\partial p}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial p}{\partial x}=0 </math> | ||
:<math> \frac{\partial \rho}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial \rho}{\partial x}=0 </math> | :<math> \frac{\partial \rho}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial \rho}{\partial x}=0 </math> | ||
| + | where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow. | ||
| + | :Domain [-50,50]*[-50,50] | ||
| + | :Initial Condition | ||
| + | :Boundary Condition | ||
| + | :Numerical Method | ||
| + | :Results | ||
| + | :Reference | ||
Revision as of 02:08, 8 October 2005
Problem Definition
where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow.
- Domain [-50,50]*[-50,50]
- Initial Condition
- Boundary Condition
- Numerical Method
- Results
- Reference