Diffusion term
From CFD-Wiki
(→Minimum Correction) |
(→Orthogonal Correction Approaches) |
||
| Line 69: | Line 69: | ||
In the minimum correction approach, the vectors are defined as <br> | In the minimum correction approach, the vectors are defined as <br> | ||
<math> \vec E = (\vec e \cdot \vec S_f)\cdot \vec e = S_f \cos\theta \vec e </math> <br> | <math> \vec E = (\vec e \cdot \vec S_f)\cdot \vec e = S_f \cos\theta \vec e </math> <br> | ||
| - | <math> \vec T = | + | <math> \vec T = \vec S - \vec E= S_f (\vec n - \cos\theta \vec e) </math> <br> |
[[image:Non_orthogonal_CV_minimum_correction.jpg]] <br> | [[image:Non_orthogonal_CV_minimum_correction.jpg]] <br> | ||
'''Minimum Correction Approach''' | '''Minimum Correction Approach''' | ||
==== Orthogonal Correction ==== | ==== Orthogonal Correction ==== | ||
| + | In the orthogonal correction approach, the vectors are defined as <br> | ||
| + | <math> \vec E = S_f \vec e </math> <br> | ||
| + | <math> \vec T = \vec S - \vec E = S_f (\vec n - \vec e) </math> <br> | ||
| + | [[image:Non_orthogonal_CV_orthogonal_correction.jpg]] <br> | ||
| + | '''Orthogonal Correction Approach''' | ||
| + | |||
==== Over Relaxed Correction ==== | ==== Over Relaxed Correction ==== | ||
| + | Finally, in the over relaxed approach, we define <br> | ||
| + | <math> \vec E = \frac {\vec S_f \cdot \vec S_f}{\vec S_f \cdot \vec e} \vec e = \frac {S_f}{\cos \theta} \vec e </math> <br> | ||
| + | <math> \vec T = \vec S - \vec E = S_f (\vec n - \frac{1}{\cos \theta} \vec e) </math> <br> | ||
| + | [[image:Non_orthogonal_CV_Over_relaxed_correction.jpg]] <br> | ||
| + | '''Over Relaxed Correction Approach''' | ||
== References == | == References == | ||
Revision as of 05:21, 5 December 2005
Contents |
Discretisation of the Diffusion Term
Description
For a general control volume (orthogonal, non-orthogonal), the discretization of the diffusion term can be written in the following form
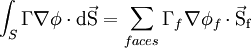
where
- S denotes the surface area of the control volume
denotes the area of a face for the control volume
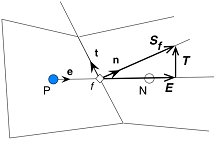
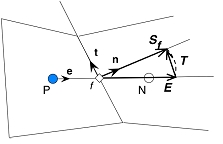
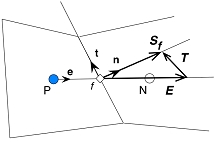
As usual, the subscript f refers to a given face. The figure below describes the terminology used in the framework of a general non-orthogonal control volume
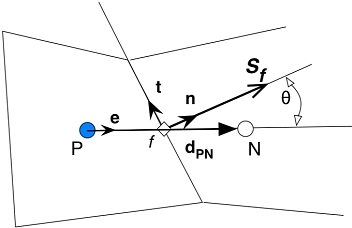
A general non-orthogonal control volume
Note: The approaches those are discussed here are applicable to non-orthoganal meshes as well as orthogonal meshes.
A control volume in mesh is made up of set of faces enclosing it. Where represents the magnitude of area of the face. And n represents the normal unit vector of the face under consideration.
If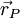 
and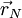 
are position vector of centroids of cells P and N respectively. Then, we define
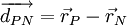
We wish to approaximate the diffusive flux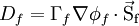 
at the face.
Approach 1
A first approach is to use a simple expression for estimating the gradient of a scalar normal to the face.
![D_f = \Gamma _f \nabla \phi _f \cdot \vec S_f = \Gamma _f \left[ {\left( {\phi _N - \phi _P } \right)\left| {{{\vec S_f} \over {\overrightarrow{d_{PN}}}}} \right|} \right]](/W/images/math/2/2/f/22f7fe72fd16546ff2d65bf48adf7a35.png)
where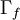 
is a suitable face average.
This approach is not very good when the non-orthogonality of the faces increases. If this is the case, it is advisable to use one of the following approaches.
Approach 2
We define the vector
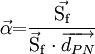
giving us the expression:
![D_f = \Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _N - \phi _P } \right)\vec \alpha \cdot {\rm{\vec S_f + }}\bar \nabla \phi_f \cdot {\rm{\vec S_f - }}\left( {\bar \nabla \phi_f \cdot {\overrightarrow{d_{PN}}}} \right)\vec \alpha \cdot {\rm{\vec S_f}}} \right]](/W/images/math/7/c/f/7cf1e0cce420c5d8f260ea5c7f3340ff.png)
where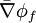 
and 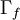are suitable face averages.
Orthogonal Correction Approaches
In non-orthogonal grids, the gradient direction that will yield an expression involving the values at the neighboring control volumes will have to be along the line joining the centroids of the two control volumes. If this direction has a unit vector denoted by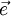 
then, by definition
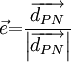
then the gradient in the direction of 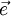can be written as
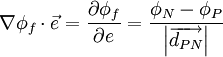
If the surface vector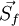 
is written as the summation of two vectors 
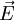and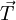 
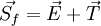
where 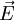is in the direction joining the centroids of the two control volumes, we will then be able to express the diffusive flux in terms of the neighboring control volumes plus an additional correction. This is done as follows
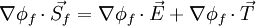
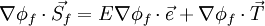.... (where E is the magnitude of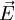 
At the outset, one obtains
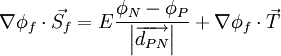
The first term in the above equation can be thought of as the orthogonal contribution to the diffusive flux, while the second term represents the non-orthogonal effects. At this point, the vector 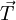has not been defined yet. There are three main methods to define this vector.
Minimum Correction
In the minimum correction approach, the vectors are defined as
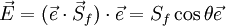
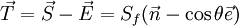
Minimum Correction Approach
Orthogonal Correction
In the orthogonal correction approach, the vectors are defined as
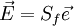
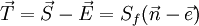
Orthogonal Correction Approach
Over Relaxed Correction
Finally, in the over relaxed approach, we define
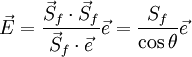
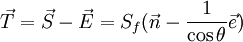
Over Relaxed Correction Approach
References
- Ferziger, J.H. and Peric, M. (2001), Computational Methods for Fluid Dynamics, ISBN 3540420746, 3rd Rev. Ed., Springer-Verlag, Berlin..
- Hrvoje, Jasak (1996), "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows", PhD Thesis, Imperial College, University of London (download).
Return to Numerical Methods
