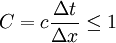Courant–Friedrichs–Lewy condition
From CFD-Wiki
Common
It is an important stability criterion for hyperbolic equations.
The one-dimensional case
For one-dimensional case, the CFL has the following form:
|
| (2) |
where C is called the Courant number
where the dimensionless number is called the Courant number,
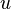is the velocity (whose dimension is Length/Time)
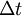is the time step (whose dimension is Time)
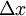is the length interval (whose dimension is Length).
The value of 
changes with the method used to solve the discretised equation. If an explicit (time-marching) solver is used then typically 
. Implicit (matrix) solvers are usually less sensitive to numerical instability and so larger values of may be tolerated.
Courant, R., K. O. Fredrichs, and H. Lewy (1928), "Uber die Differenzengleichungen der Mathematischen Physik", Math. Ann, vol.100, p.32, 1928.
Anderson, Lohn David (1995), "Computational fluid dynamics: the basics with applications", McGraw-Hill, Inc.
