Lid-driven cavity problem
From CFD-Wiki
Introduction
The lid-driven cavity problem has long been used a test or validation case for new codes or new solution methods. The problem geometry is simple and two-dimensional, and the boundary conditions are also simple. The standard case is fluid contained in a square domain with Dirichlet boundary conditions on all sides, with three stationary sides and one moving side (with velocity tangent to the side).
Add picture here
Since this case has been solved many times, there is a great deal of data to compare with. A good set of data for comparison is the data of Ghia, Ghia, and Shin (1982), since it includes tabular results for a number of Reynolds numbers. Other researchers have solved the problem under laminar and turbulent conditions, and aspect ratios other than one have also been used. This problem is also sometimes referred to as the shear-driven cavity problem, though the shear-driven cavity is technically a different problem.
Sample Results
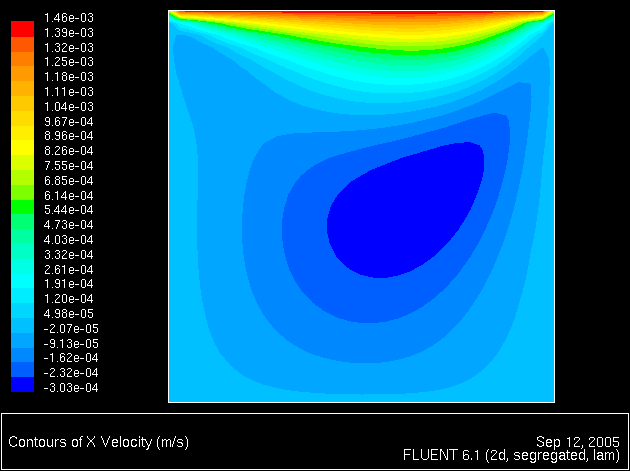
Shown below are a few results from a simulation of the lid-driven cavity (for a Reynolds number of one hundred) using the commercial Fluent code.
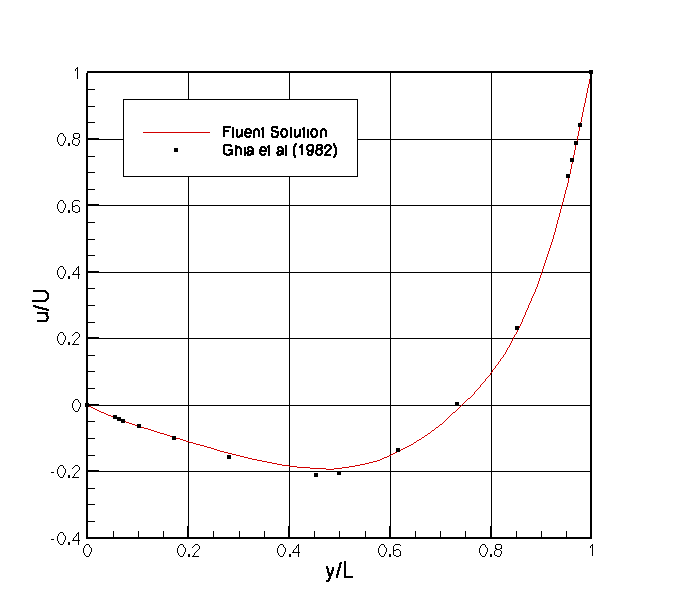
The 32x32 grid used here is somewhat coarse, as can be seen in the upper left and right corners of the contour plot. Increasing the grid resolution would improve the look of the contour plot somewhat, but since the boundary conditions are not smooth at these corners we will probably always have some issues there. In spite of this issues, we do a reasonable job matching the Ghia et al (1983) results, as shown below.
Here we have plotted u/U on the vertical line x/L = 0.5. We have reasonably good agreement with the previous results.
References
- Ghia, Ghia, and Shin, "High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method", Journal of Computational Physics, Vol. 48, pp. 387-411, 1982.