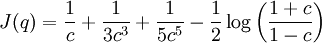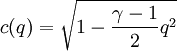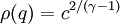Ringleb flow
From CFD-Wiki
-
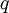 = magnitude of velocity
= magnitude of velocity
-
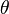 = angle between velocity and
= angle between velocity and 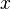 -axis
-axis
-
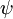 = stream function
= stream function
Take
to be constant as a streamline.
Streamline equations:
where
References
- Shapiro ({{{year}}}), Mechanics and Thermodynamics of Compressible flows, {{{rest}}}.