Introduction to turbulence/Turbulence kinetic energy
From CFD-Wiki
It is clear from the previous chapter that the straightforward application of ideas that worked well for viscous stresses do not work too well for turbulence Reynolds stresses. Moreover, even the attempt to directly derive equations for the Reynolds stresses using the Navier-Stokes equations as a starting point has left us with far more equations than unknowns. Unfortunately this means that the turbulence problem for engineers is not going to have a simple solution: we simply cannot produce a set of reasonably universal equations. Obviously we are going to have to study the turbulence fluctuations in more detail and learn how they get their energy (usually from the mean flow somehow), and what they ultimately do with it. Our hope is that by understanding more about turbulence itself, we will gain insight into how we might make closure approximations that will work, at least sometimes. Hopefully, we will also gain an understanding of when and why they will not work.
An equation for the fluctuating kinetic energy for constant density flow can be obtained directly from the Reynolds stress equation derived earlier, equation 3.35, by contracting the free indices. The result is:
|
| (4.1) |
where the incompressibility condition ( 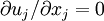 ) has been used to eliminate the pressure-strain rate term, and
) has been used to eliminate the pressure-strain rate term, and 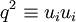 .
.
The last term can be simplified by recalling that the velocity deformation rate tensor,  , can be decomposed into symmetric and anti-symmetric parts; i.e.,
, can be decomposed into symmetric and anti-symmetric parts; i.e.,
|
| (4.2) |
where the symmetric part is the strain-rate tensor, 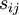 , and the anti-symmetric part is the rotation-rate tensor
, and the anti-symmetric part is the rotation-rate tensor  , defined by:
, defined by:
|
| (4.3) |
Since the double contraction of a symmetric tensor with an anti-symmetric tensor is identically zero, it follows immediately that:
|
| (4.4) |
Now it is customary to define a new variable k, the average fluctuating kinetic energy per unit mass, by:
|
| (4.5) |
By dividing equation 4.1 by 2 and inserting this definition, the equation for the average kinetic energy per unit mass of the fluctuating motion can be re-written as:
|
| (4.6) |
The role of each of these terms will be examined in detail later. First note that an alternative form of this equation can be derived by leaving the viscous stress in terms of the strain rate. We can obtain the appropriate form of the equation for the fluctuating momentum from equation 3.21 by substituting the incompressible Newtonian constitutive equation into it to obtain:
|
| (4.7) |

![\begin{matrix}
\left[ \frac{\partial}{\partial t} \left\langle u_{i} u_{i} \right\rangle + U_{j} \frac{\partial }{\partial x_{j} } \left\langle u_{i} u_{i} \right\rangle \right] \\
& = & \frac{\partial}{\partial x_{j}} \left\{ -\frac{2}{\rho} \left\langle p u_{i} \right\rangle \delta_{ij} - \left\langle q^{2} u_{j} \right\rangle + 4 \nu \left\langle s_{ij} u_{i} \right\rangle \right\} \\
& & - 2 \left\langle u_{i}u_{j} \right\rangle \frac{\partial U_{i}}{\partial x_{j}} - 4 \nu \left\langle s_{ij} \frac{\partial u_{i}}{\partial x_{j} } \right\rangle \\
\end{matrix}](/W/images/math/c/d/d/cdd713e7c866ab3a41c1db5df222a7b2.png)

![\omega_{ij} = \frac{1}{2} \left[ \frac{\partial u_{i}}{\partial x_{j}} - \frac{\partial u_{j}}{\partial x_{i}} \right]](/W/images/math/b/7/7/b771bd4a8422189e342acf06c33672da.png)
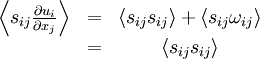
![k \equiv \frac{1}{2} \left\langle u_{i}u_{i} \right\rangle = \frac{1}{2} \left\langle q^{2} \right\rangle = \frac{1}{2} \left[ \left\langle u^{2}_{1} \right\rangle + \left\langle u^{2}_{2} \right\rangle + \left\langle u^{2}_{3} \right\rangle \right]](/W/images/math/5/f/4/5f49df0b6717a9a52c142a281cda814f.png)
![\begin{matrix}
\left[ \frac{\partial}{\partial t} + U_{j} \frac{\partial}{\partial x_{j}} \right] k & = & \frac{\partial}{\partial x_{j}} \left\{ - \frac{1}{\rho} \left\langle pu_{i} \right\rangle \delta_{ij} - \frac{1}{2} \left\langle q^{2} u_{j} \right\rangle + 2 \nu \left\langle s_{ij}u_{i} \right\rangle \right\} \\
& & - \left\langle u_{i}u_{j} \right\rangle \frac{\partial U_{i}}{\partial x_{j} } - 2 \nu \left\langle s_{ij} s_{ij} \right\rangle \\
\end{matrix}](/W/images/math/d/3/e/d3e5c43dd0769a3aad2fa9455ba955af.png)
![\left[ \frac{\partial }{\partial t } + U_{j} \frac{\partial }{\partial x_{j} } \right] u_{i} = - \frac{1}{\rho} \frac{\partial p}{\partial x_{i}} + \nu \frac{\partial^{2} u_{i}}{ \partial x^{2}_{j}} - \left[ u_{j} \frac{\partial U_{i}}{\partial x_{j} } \right] - \left\{ u_{j} \frac{\partial u_{i}}{ \partial x_{j}} - \left\langle u_{j} \frac{\partial u_{i}}{\partial x_{j}} \right\rangle \right\}](/W/images/math/e/0/b/e0b4576b17fa45fb1c66a20067c611f4.png)