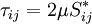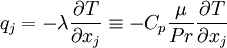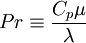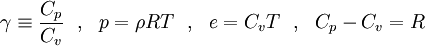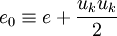Navier-Stokes equations
From CFD-Wiki
The Navier-Stokes equations are the basic governing equations for a viscous, heat conducting fluid. It is a vector equation obtained by applying Newton's Law of Motion to a fluid element and is also called the momentum equation. It is supplemented by the mass conservation equation, also called continuity equation and the energy equation. Usually, the term Navier-Stokes equations is used to refer to all of these equations.
Contents |
History
Claude Louis Marie Henri Navier’s name is associated with the famous Navier-Stokes equations that govern motion of a viscous fluid. He derived the Navier-Stokes equations in a paper in 1822. His derivation was however based on a molecular theory of attraction and repulsion between neighbouring molecules. Euler had already derived the equations for an ideal fluid in 1755 which did not include the effects of viscosity. Navier did not recognize the physical significance of viscosity and attributed the viscosity coefficient to be a function of molecular spacing.
The equations of motion were rederived by Cauchy in 1828 and by Poisson in 1829. In 1843 Barre de Saint-Venant published a derivation of the equations that applied to both laminar and turbulent flows. However the other person whose name is attached with Navier is the Irish mathematician-physicist George Gabriel Stokes. In 1845 he published a derivation of the equations in a manner that is currently understood.
Equations
The instantaneous continuity equation (1), momentum equation (2) and energy equation (3) for a compressible fluid can be written as:
|
| (1) |
|
| (2) |
|
| (3) |
![\frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0](/W/images/math/0/7/1/071e4f5508fd336ddad848551ce3188e.png)
![\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0, \quad i=1,2,3](/W/images/math/a/b/1/ab156ace613d48ef91f8457e27a51aad.png)
![\frac{\partial}{\partial t}\left( \rho e_0 \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_j e_0 + u_j p + q_j - u_i \tau_{ij} \right] = 0](/W/images/math/8/1/7/8176cdf87a72617542883cbbeafc50cc.png)
For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous stress is given by:
|
| (4) |
Where the trace-less viscous strain-rate is defined by:
|
| (5) |
The heat-flux, 
, is given by Fourier's law:
|
| (6) |
Where the laminar Prandtl number 
is defined by:
|
| (7) |
To close these equations it is also necessary to specify an equation of state. Assuming a calorically perfect gas the following relations are valid:
|
| (8) |
Where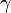 
, 
, 
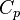and 
are constant.
The total energy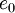 
is defined by:
|
| (9) |
Note that the corresponding expression (15) for Favre averaged turbulent flows contains an extra term related to the turbulent energy.
Equations (1)-(9), supplemented with gas data for , ,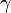 
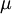and perhaps , form a closed set of partial differential equations, and need only be complemented with boundary conditions.
== Boundary conditions ==10
Existence and uniqueness
The existence and uniqueness of classical solutions of the 3-D Navier-Stokes equations is still an open mathematical problem. In 2-D, existence and uniqueness of regular solutions for all time have been shown by Jean Leray in 1933. He also gave the theory for the existence of weak solutions in the 3-D case while uniqueness is still an open question.
References
C. L. M. H. Navier (1822), "Memoire sur les lois du mouvement des fluides", Mem. Acad. Sci. Inst. France, 6, 389-440.
